应聘某一岗位没被录用？原因可以有很多：个人职业期望与岗位不符；能力尚未达标。但你是否想过，你被拒绝的理由竟是性格测试没通过！算法正在影响我们的工作和生活，其规模、重要程度，隐秘性，使得这种影响不再普通。不仅如此，算法出错了还不好伸冤，而且研究显示，算法对穷人有歧视。
Cathy O’Neil 是约翰逊实验室高级数据科学家、哈佛大学数学博士、麻省理工学院数学系博士后、巴纳德学院教授，曾发表过大量算术代数几何方面的论文。他曾在著名的全球投资管理公司D.E. Shaw担任对冲基金金融师，后加入专门评估银行和对冲基金风险的软件公司 RiskMetrics。
几年前，一个叫Kyle Behm的年轻人由于躁郁症中途辍学，离开他就读的范德比尔特大学，该学校位于田纳西州纳什维尔。一年半后，Kyle康复了，并回到另一所大学继续他的学业。在那时，他从一个朋友那儿了解到一份兼职工作：在Kroger超市打工，尽管工资相当低，但Kyle愿意做。Kyle的朋友正好辞职，并愿意为他做担保。对于像Kyle这样学习优异的学生来说，担保就是走走形式。
然而Kyle并没有接到面试通知。他询问他的朋友，他的朋友解释说：Kyle的性格测试结果显示，他被列入“红灯区”。Kyle做的测试是由总部位于波士顿的人力资源管理公司Kronos开发，作为人力选拔员工的一部分。Kyle把这件事情告诉了他的律师父亲，他的父亲问他测试题问了些什么。Kyle说和他在医院里做的题类似，就是“五因素模型”这类的问题。根据外向性，随和性，谨慎性，情绪稳定性以及开放性评分。
起初，由于测试题丢掉一份工资低廉的工作并不是什么大问题。Roland Behm鼓励他的儿子继续找。但Kyle被一次次拒绝。他应聘的每一家公司用的是同一套测试题，到最后他也没收到一个offer。
Roland Behm也不知所措。心理健康问题似乎严重影响他儿子的就业。研究之后他发现：性格测试题在大型的招聘公司之间非常普遍，尽管在法律上并无实际意义。他解释说：很少有人找工作因为测试结果被列入红灯区。即便他们被“红灯”了，他们也不会想着去找律师。
Behm给包括Home Depot和Walgreens在内的七家公司发了通知，倡议通过集体诉讼来抵制测试招人的违法行为。在我写这篇文章的时候，起诉讼仍在跟进。此次争议主要在于Kronos的测试是否有医学依据；另依据1990年颁布的美国残疾人法案，该行为是违法的。如果诉讼成功，法院不得不就招聘公司或Knoros是否违反美国残疾人法做出判决。
然而，问题不再是这些公司是否需要担责这么简单，基于复杂数学公式的自动化系统在发达国家逐渐普遍。其规模、重要程度，隐秘性，使得算法把一个人普通的生活变得不再普通。
更多算法知识：www.yangfenzi.com/tag/suanfa
大可不必这样。金融危机后，数学家们所谓的“魔法公式”再一次带来房贷危机，导致一些重要的金融机构倒闭。如果足够理智，我们完全能够阻止类似事件再次发生。可事实却是，新科学技术大热，甚至拓展到更多领域。他们不仅关注全球经济市场，还关注人类。数学家和统计学家正在研究人类的欲望，行为和消费模式。他们预测我们的诚实度，计算我们成为学生，工人，情人，罪犯的可能性。
这是大数据经济，寻求利益最大化。一个计算机程序可以在数千份简历或申请表中运行，获得一份简单明了的表单，最佳候选人位于表单首行。既省时又公正客观。不受人类偏见的影响，就是机器编译代码。2010年左右，数学已经渗透到人类的生活中，受到一众人的青睐。
大多数算法被应用在好的方面。目的是用客观测量代替主观判断——也可能是找出学校里教学最差的教师，或预测一个罪犯二次进监狱的概率有多大。
算法的解决方案主要针对真正存在的问题。一个学校的校长不能总是针对问题老师，因为他们也是朋友。法官是人，是人就会有偏见，有偏见就会导致他们无法做到完全公平。举个例子，午餐前法官们会感到饥饿，饥饿会让他们的判决比平时更苛刻。所以加强人机的一致性十分重要，尤其是当你觉得新系统听起来尚且科学。
难的是最后一部分。只有少数的算法和评分系统经过严格的科学检测，而且我们有充分的理由怀疑他们无法通过测试。举个例子，自动化教师的测评每年都可能不同。蒂姆·克里夫在纽约当了26年的中学英语教师，却从未改变过自己的教学风格。当然，如果分数不重要，那是一回事。但事实却是教师往往都被解雇了。
除了法官的裁决，我们有其他的理由担忧被告被判决有罪。将数据注入算法。其他类型的输入往往也会出现问题，而且更麻烦。一些法官甚至会询问被告家里是否有人有前科，这明显有失公平。
不仅如此，如果你的信用评分较低或无任何不良驾驶记录，你可以用算法决定交多少保险；或者关于贷款条款我们会收到哪类政治信息，我们都会用到算法。算法可以预测天气，然后决定人们的工作行程，减少他们送孩子去医院或者学校可能浪费的时间。
其受欢迎程度依赖于它们是客观的概念，而算法影响数据经济基于人类会犯错误。尽管他们被用在好的事情上，算法还是会把人们的偏见，误解编译到自动化系统里影响我们的生活。就像上帝一样，这些数学模式并不透明，他们的工作原理仅对数学家和计算机科学家可见。判决即使错了也不容争议。往往穷人被惩罚压迫，富人越来越富。
撇开公平性和合法性的问题，研究表明，性格测试并不能很好的预测一个人的工作表现。Roland Behm表示：测试的最初目的并不是招聘好员工，就是为了尽可能多的筛掉人。
你可能认为性格测试很好做。其中一个问题是：“经常会有情绪的波动？”你应该回答“不会”。另一个问题“很容易生气？”你也要回答“不会”。
事实上，企业通过这种方式筛选求职者也会遇到麻烦。监管机构发现，CVS连锁药店通过性格测试要求人们回答诸如“人们做哪些事让你愤怒”，“有亲密的朋友没有任何用；他们总是让你失望”等问题，非法筛选出有心理疾病的应聘者。
Kroger的问题更简单一些：哪一个形容词更能描述你工作时的状态：独一无二还是井井有条？如果回答独一无二，说明你高度开放，自恋；如果你回答井井有条，说明你自觉，自我控制能力强。
想象一下：Kyle Behm被roger拒绝后到麦当劳工作。他成为星级雇员。在厨房管理四个月，一年后拿到整个分店的专营权。这个时候，Kroger会不会有人重新审视当年的性格测试错的离谱。
幸运的是，广大求职者并未因自动化系统被拒绝。但他们依旧面临者简历被筛掉或者面试等挑战。这些问题一直困扰着少数族裔和妇女。
规避这种偏见的理想方法就是不对申请人上纲上线。20世纪70年代，音乐家只要以男性为主。当种族，名望不再重要时，女性音乐家开始出现，虽然仅占总数的四分之一。
求职者一定要让面试官对自己的简历过目不忘。做到简洁有针对性。简历中可以包括之前从事的职位（销售经理，软件构架师），语言（普通话，Java），或者荣誉（成绩优异）。
【来源：《卫报》作者：Cathy O’Neil 译者：郭雅菲】
·氧分子网（http://www.yangfenzi.com）延伸阅读：
➤ Facebook开源深度学习框架Torchnet与谷歌TensorFlow有何不同
➤ 地平线机器人李星宇：复杂的中国驾驶场景，正是深度学习的优势
➤ 百度吴恩达谈深度学习局限：AI经济价值目前仅来自监督学习
➤ 张佳晨：头条号的这个小动作，暴露了今日头条算法分发的短板
➤ 卡耐基梅隆大学邢波：为人工智能装上引擎—忆格拉丹东登山之旅
Yao’s protocol.
「如何让两个女士比较出谁更胖——在她们都不想泄漏体重的前提下？」
问题是这样的：假设 Alice 手上有一个隐私函数 f，Bob 有隐私数据 x，那么请为他们设计一个协议，让双方互相不给任何人透露自己隐私的情况下，计算出 f(x) 的数值？（从 f(x) 的结果推断 x 或者 f 不算在内；双方始终遵守协议。）
实现是这样的：考虑一个 k 个 bit 到一个 bit 的简单函数 f（更复杂的函数可以简化到这个样子），alice 可以打出 f 的真值表来，然后她产生 k+1 对随机数，表示 k 个输入 bit（）和输出 bit 的 0/1 值（）。
接着她按照这些随机数加密真值表，比如如果 f(1, 1)=0，则她用两个随机数作为密钥加密产生一个密文。她可以把加密的真值表连同表示结果的随机数发给 Bob。
接下来 Bob 需要按照自己的数据（x）找 Alice 要 k 个随机数解码他拿到的真值表，真值表中只有一项可以被解码，解码的结果就是 f(x)，其他的则无法解码。
要随机数的过程是基于 Oblivious Transfer，这个协议要求：
Bob 根据自己的选择获取 Alice 两条私密消息中的一条，另一条则无法解密；
而 Alice 不能得知 Bob 的选择。
过程是：
Alice 生成 RSA 公钥-密钥对，她把公钥发给 Bob，Bob 根据自己的选择获取。以下计算均在上进行。
Alice 生成两个随机数发给 Bob。
Bob 生成随机数 k，计算发给 Alice。由于 k 是私密的，Alice 无法解密出 c 来。
Alice 计算，发送给 Bob。
Bob 计算（因为），而对于另一条消息，他就无法成功解码。
有关 @aricatamoy「为什么不用天平」，那么请问：两个人该怎么做才能保证天平上面没被动过手脚，暗地里收集她们的体重呢？
我们从一个简单的算法题开始考虑：给出k个有序的数组 ，每一个长度为n；你可以对该数组进行线性时间的预处理，然后回答如下询问：给出x，回答每个数组中第一个小于x的元素是什么。
常规的想法是对于每个数组二分查找，复杂度是，而fractional cascading通过一个简单的idea允许我们做到。
进行如下的预处理：令；然后递归构造对于每一个，令为将数组的全部元素与中偶数位置的元素归并而得到的新数组。这个预处理可以在线性时间内完成，因为我们发现对于任何 i 满足 。
同时每个元素计算左右两个指针，对于中的元素（上一段中，它是通过两个有序数组归并得到的）：
1) 如果来自，则维护左右第一个来自的元素的位置；
2) 如果来自，则维护左右第一个来自的元素的位置；
这类指针可以在线性时间内通过递推求得。
对于询问x，首先在中二分并使用指针找到对应的位置。然后利用左右指针p1 p2，找到对应在中的位置。由于p1 p2在中一定只隔一个元素，故我们只要扫描常数个位置就能找到中的第一个小于x的元素（且原本属于）。以此类推，得到了的答案后，只要常数时间就能得到的答案。故总的时间复杂度为，即第一次使用了二分，之后每次都是常数查找。
该方法还使用于range tree 和 half-plane range reporting data structure（给出平面上一些直线，构造一个线性空间的数据结构，可以在的时间内回答一个点的上方有哪些直线，这里m是答案数量）等等数据结构中来优化掉一个log n因子。
并查集的路径压缩:
并查集是用来解决集合查询/合并问题的经典方案，
它构造了一个森林，森林中每棵树代表一个集合。
初始时对于所有的节点设 x.parent = x，表示每个节点都是树根，代表一个集合。
查询一个节点所属集合时，递归返回节点所在树的根节点:
def find(x):
if x.parent != x:
return find(x.parent)
return x
合并时只需将一个节点的根的parent指向另一个根,
这样就把两棵树合并为了一棵
def union(x,y):
xRoot = find(x)
yRoot = find(y)
xRoot.parent = yRoot
并查集本身是一个巧妙的设计，
但随着不断的union操作容易带来树深度过深，
导致效率降低的问题(查询操作复杂度为树的深度)，
于是就有个神奇的路径压缩策略，
只对find算法进行了小改:
def find(x):
if x.parent != x:
x.parent = find(x.parent)
return x.parent
增加一个更新x.parent操作，
每次查询之后，从根到x的长度为k的路径，将更新为k条长度为1的路径，
使得并查集的操作从O(n)直接降到了介于与的一个值。
具体的复杂度分析见
Cormen, Thomas H. Introduction to algorithms. MIT press, 2009. 这本书的21.3，
只使用路径压缩的话，
执行n次初始化,最多n-1次union，与m次find的总时间，在最坏情况下是
上述章节里还讨论了另外的一些优化，感兴趣的同学可以自行阅读。
当年是在做一道需要反复查询的题的时候，
自己YY出了集合查询的基本思路(跟基础并查集差不多，不过是非递归的)，
但是受困于每次查询节点的O(n)的操作，无法AC，
然后有人告诉我这道题用"并查集"可以解决，
查了一下资料之后，惊为天人…
不得不说前人的智慧实在太强大…
在有启发式合并的优化下才是ackermann函数的反函数的时间复杂度 但只考虑路径压缩的情况下也是一个比logN小的值已经忘了之前讨论的问题是啥了，如果说比以2为底小没问题，但是如果套上了Theta，好像底已经没有意义了，因为底是可以换的，于是就一样大了并查集的路径压缩，实际上只是相当于WAM里的unification的实现。SPFA (Shortest Path Faster Algorithm)
说到单源最短路径，大家常常会想到的是Dijkstra算法（发音： 荷兰语：[ˈɛtsxər ˈʋibə ˈdɛikstra] ）。但是对于带有负权的单源最短路径的话，可能就只能求助于Bellman Ford算法了。但是BF算法的时间复杂度是，有没有更快的解决办法呢？
这里就要介绍一下西南交通大学的段凡丁于1994年发表的《关于最短路径的SPFA快速算法》了。SPFA算法的在该篇文章中的期望时间复杂度的证明据说是错误的，但是因为其杰出的实际运行效率和简单的实现而让ACMer都推崇备至。
Dijkstra算法中的队列保存的是所有未确定的点，所以需要每次从中选取最短路径估计最小的顶点的邻边来进行松弛。而SPFA算法中的队列保存的是所有松弛过的边对应的顶点。上述两种算法与BF算法相比，优势都体现在不是盲目地对所有边进行松弛，故可以得到比BF算法更好的性能结果。
但是Dijkstra算法中的最短路相当于在一点一点“生长”，如果出现负权边，那么个生长的过程就需要绕回去，这对于Dijkstra算法来说是做不到的。而BF算法并不是依靠这种“生长”的办法，所以它可以做到这一点。因此，SPFA作为BF算法的队列优化版，解决了Dijkstra算法面对负权边的问题，又避免了BF算法在性能上的劣势，是一个实际运用中很受欢迎的算法。
跳表：
由于链表不是call-by-rank而是call-by-position的一类线性数据存储结构。所以链表的查找没有办法应用例如有序数组中二分查找一类的方法，只能通过线性搜索进行元素的查找。
而对于一个有序链表来说，如果我们可以在查询的时候先随机跳过大量元素，再逐步减少跳跃的幅度，锁定到我们最终查找的元素上时，那么我们的搜索成本将会得到极大地减少。Skip list就是运用这个原理设计出来的。
例如上图当中，如果要搜索数字19的话，需要从左侧头结点开始，跳到下一个结点21，发现21 > 19则跳回去到下一层。下一层下一个结点为9，再后面一个是21 > 19，又跳回9并下钻。下一个结点为17 < 19则继续后跳到21，再次发生21 > 19，则往回跳到17并下钻，最后到达待搜索的节点19的位置上。
跳表有着类似平衡BST的时间复杂度，而实现更简单，常系数更小，空间占用更小。这些特点常常使得它作为平衡BST的替代品被应用。
平方根倒数速算法：
在利用到3D图形渲染的一些游戏或者程序当中，法向量的单位化计算显得尤为重要。在三维欧几里得空间当中，某一向量的单位化是指计算。其中表示向量的二范数，也即。其中设，的计算主要是乘法与加法，所以性能上不会有太大瓶颈。而计算的时候，数值求解的速度如何将会极大影响向量单位化的运行效率。平方根倒数速算法正是为了解决这个问题而出现的。
float Q_rsqrt(float x)
{
float x2 = x * 0.5F;
int i = *(int*)&x; // evil floating point bit level hacking
i = 0x5f3759df – (i >> 1); // what the fuck?
x = *(float*)&i;
x = x * (1.5F – (x2 * x * x)); // 1st iteration
return x;
}
这个方法从本质上来介绍的话，就是先近似计算一个初始值，然后带入牛顿迭代法来计算最后的较为精确的。涉及的中间变量有。首先计算i = *(int*)&x是为了获得浮点数对应的整数表示。然后利用去求出中对应的整数表示，这也就是上述注释“what the fuck”对应的那句i = 0x5f3759df – (i >> 1)的作用。
求得了整数表示以后，将该数转换回浮点数，也即求到了的近似值。最后一句使用牛顿迭代法对进行一遍迭代求解，也就是将上面得到的带入牛顿迭代法的公式当中作为初始值计算一遍，最后得到较为精确的结果。
这个算法的核心地方在于如何利用这一等式得到与的关系，而这也就是0x5f3759df的重要意义所在。具体的数学推导以及中间的“魔数”0x5f3759df是怎么算出来的可以参见维基百科Fast inverse square root。
珠排序：
珠排序作为一种自然排序算法，在计算机当中没有办法找到一种很好的实现来进行模拟，但是，并且只能为正整数序列进行排序。但是其中的思路却真的算是一种奇技淫巧了。
对个正整数进行排序的话，我们就造根柱子。然后对于每一个正整数，我们就把它想象成个珠子。我们将这个珠子分别串在在第1根、第2根、……第根柱子上。
所有数都串完了以后，将这根柱子垂直放置下来，所有珠子都随重力下落，然后每行上（不是每根柱子上）的珠子数，就是最后的排序结果。
Duff’s Device：
{
从一个指针from向另一个指针to拷贝count个字节，你打算怎么做？
正常的做法是
do {
*to++ = *from++;
} while(–count > 0);
这段代码当中，这句–count > 0的会被判断count次。
那么真的需要判断这么多次么？让我们来看看Duff’s Device的实现是怎么做的
void send(int *to, int *from, int count)
{
int n = (count + 7) / 8;
switch (count %
case 0 : do { *to++ = *from++;
case 7 : *to++ = *from++;
case 6 : *to++ = *from++;
case 5 : *to++ = *from++;
case 4 : *to++ = *from++;
case 3 : *to++ = *from++;
case 2 : *to++ = *from++;
case 1 : *to++ = *from++;
} while (–n > 0);
}
}
这段代码巧妙地将switch和while杂糅在一起，不仅每次8个字节进行拷贝，而且对末尾不足8个字节的部分做了精巧的处理，通过循环展开减少了循环判断的次数，从而优化了性能。
尾递归：
给你一个单链表的头结点，让你得到这条链表的长度是多少，要求用递归进行编写的话，你会怎么做呢？
正常的做法是
int linked_list_length(node *head)
{
if (head->next == NULL)
return 0;
else
return linked_list_length(head->next) + 1;
}
这段代码的问题在于什么呢？如果链表非常长的话，成百上千次的递归压栈将会耗尽栈空间，造成栈溢出。如果我们使用尾递归的话，就可以这样
int linked_list_length(node *head, int len)
{
if (head->next == NULL)
return len;
else
return linked_list_length(head->next, len + 1);
}
尾递归与普通递归最大的区别在于，整个递归调用占据了整个return后面的部分。由于它在整个方法的最后才被调用，那么之前函数压栈保留的所有局部变量等等信息都不影响下一次递归调用，所以本次方法中栈内的信息可以被清空，让下次调用可以重复使用这段栈空间。
所以尾递归的本质，其实就是将这次递归方法当中的必要信息，传递到下次递归当中，从而保证return后面是一个完整的递归函数调用而不是一个表达式。
二级指针删除单向链表中结点：
这个利用二级指针（pointers-to-pointers）优化单向链表当中的删除操作，是Linus在Linus Torvalds Answers Your Questions上就什么才是真正的“core low-level kind of coding”所提出的一个例子。当你要写一个单向链表当中根据某个特定条件来剔除结点的函数，你会怎么写呢？
正常的做法是
typedef bool (*remove_fn)(const node *n);
void remove_if(node *head, remove_fn rm)
{
for (node *prev = NULL, *curr = head; curr != NULL; )
{
node* next = curr->next;
if (rm(curr))
{
if (prev) prev->next = next;
else head = next;
delete curr;
}
else
prev = curr;
curr = next;
}
}
其中remove_fn是一个函数指针类型，表示判断是否删除结点的条件。这里的实现通过维护一个prev指针来进行结点的删除，需要判断prev是否为NULL来确定当前删除的结点是不是头结点。这种实现方式是被Linus所唾弃的“This person doesn’t understand pointers”。那么使用二级指针对上述代码进行优化的话，就是
void remove_if(node **head, remove_fn rm)
{
for (node **curr = head; *curr; )
{
node *entry = *curr;
if (rm(entry))
{
*curr = entry->next;
delete entry;
}
else
curr = &entry->next;
}
}
上述代码的重点在于二级指针curr。循环开始时，二级指针curr指向头结点的指针。如果头结点是需要删除的结点的话，*curr=entry->next就相当于*head=(*head)->next，也即修改头结点的指针指向下一个结点。
如果要删除的节点不是头结点的话，由于curr是通过&entry->next更新的，所以要此时curr指向要删除的节点的上一个节点的next指针，而entry指向的是要当前要删除的指针，此时*curr=entry->next就相当于prev->next=entry->next，从而完成当前节点的删除。
如何判断一个链表中有闭环？
如果有闭环，如何确定闭环的起始节点？
这个问题是我们数据结构课的老师(同时还是学校ACM队教练)在课堂上让我们讨论研究的，整整讨论了一节课吧。其基本知识仅仅是链表，但这个问题却非常有意思。大家不断讨论中，各种方法越来越优化，最后的最佳算法真是让人眼前一亮。
后来实习面试时，一面考官在问了一堆简单的排序算法后说要问我一个难一点的问题，然后就问了上述的第一个问题。我说了答案后顺便还说了第二个问题的答案。他一脸惊讶地问我是不是遇到过，我告诉他我们上课讲过…
簡單、無遞歸，保障時間複雜度
!= x)
= djs[djs 
], x = djs 
;
int find(x)
{
while (djs
djs
return x;
}
`Variant` segment tree (學名不明)區間表示
從[0,n)開始，每次使用 floor((l+h)/2) 的區間折半策略。如 [0,5) 得到 [0,2) [2,5) [0,1) [1,2) [2,3) [3,5) [3,4) [4,5)。
可以用如下映射法則給區間編號：
int id(int l, int h)
{
return l == h-1 ? 2*n+l : l+h;
}
給定 x，枚舉滿足 (y & x) == y 的 y
for (int y = x; ; y = y-1 & x) {
// process y
if (! y) break;
}
所有m位01串中枚舉包含mm個1的
int large = (1<<mm)-1 << m-mm, g = (1<<m)-1, h;
for(;;) {
// process g
if (g == large) break;
h = (g | g-1) + 1;
g = h | (h&-h)-1 >> __builtin_ctz(g)+1;
}
32-1-__builtin_clz(x) 計算 floor(log2(x))
Topological sort
degree向量中減少爲0的元素可以組織成一個棧
for (i=0; i<n; i++)
)
++
)
= top, top = i;
)
)
= top, top = u;
for (auto j: e
d
top = -1
for (i=0; i<n; i++)
if (! d
d
while (top != -1) {
v = top
top = d[top]
// process v
for (auto u: e
if (! –d
d
}
Sieve of Eratosthenes 求 Euler phi
== i)
= phi 
/i*(i-1);
iota(phi, phi+n, 0);
for (i=2; i<n; i++)
if (phi
for (j=i; j<n; j+=i)
phi
Fenwick tree (我喜歡下標從0開始)
+= y;
void add(int x, int y)
{
for (; x < n; x |= x+1)
fenwick
}
// sum of [0,x)
void getSum(int x)
{
int s = 0;
for (; x; x &= x-1)
s += fenwick[x-1];
return s;
}
實際上 add 可以從遞增變爲遞減，而 getSum 從遞減變爲遞增
void add(int x, int y)
{
for (x++; x; x &= x-1)
fenwick[x-1] += y;
}
// sum of [x,n)
;
void getSum(int x)
{
int s = 0;
for (; x < n; x |= x+1)
s += fenwick
return s;
}
Binary heap 根據鍵查位置
make_heap push_heap pop_heap 等，重載 operator= 再根據 this 指針更新鍵到位置的映射。實際上沒啥用，自己實現更方便
在那個NOIP/NOI不能用STL的年代，我琢磨了怎麼重載操作符使 stl_set.h 支持節點size信息。但STL實現的節點指針修改推測不是可組合的，很難實現。
Treap類似Splay維護dynamic sequence
在查詢區間兩端插入低priority的節點，使得區間對應的節點形成一棵子樹並被提升到接近根的位置，可以直接讀出monoid和信息。
這樣做不清楚時間複雜度會變成什麼樣。
Top-down Splay tree
top-down Splay tree可以額外維護monoid域，left/right spine表示的節點如果上下倒置則可以省去parent指針，參見<fxr.watson.org: sys/vm/vm_map.c>
如果是group的話有稍簡單的做法，無需倒置spine上的節點：<http://www.link.cs.cmu.edu/link/ftp-site/splaying/top-down-size-splay.c>
Wavelet tree
俗稱“劃分樹”。文獻中描述Wavelet tree時通常以字母表作爲劃分依據，每個區間對應一個字母表區間，當只剩一個字母時劃分結束成爲葉區間
競賽中常以rank(對於相等元素，先出現的rank小)爲劃分依據，這樣實現比較簡單。如果以字母表爲劃分依據的話，Wavelet matrix性能更高(減少了select rank操作數)
Strongly-connected components
Kosaraju’s algorithm、Tarjan’s SCC algorithm、Gabow’s SCC algorithm產生SCC的順序是topological order或逆序的，相對於收縮SCC後得到的圖而言
求2-SAT的任一方案時，根據 x 與 ~x 所在SCC的標號大小來判定 x 取 true/false。採用 Tarjan’s SCC algorithm 只需要一次DFS
Stack migration
競賽中偶有使用DFS等遞歸算法會棧溢出的情況
Windows PE可執行文件可以配置棧大小(`#pragma comment(linker, "/STACK:16777216")`)，Linux x86/64可以遷移esp/rsp
const size_t STACK_SIZE = 16*1024*1024; // ulimit -s => usually 8 MiB
char st[STACK_SIZE];
void callee()
{
int g;
scanf("%d", &g);
printf("g=%dn", g);
}
void with_stack()
{
static long sp;
asm volatile("movq %%rsp, %0nt"
"movq %1, %%rspnt"
: "=g"(sp) : "g"(st+STACK_SIZE) : "memory");
callee();
asm volatile("movq %0, %%rspnt"
: "=g"(sp) :: "memory");
}
int main()
{
with_stack();
}
對編譯器瞭解很少，某些用例可能需要修改這個代碼
比如某些情況下棧會標記爲可執行，此時需要標記`st`所在segment權限可執行等。
Shunting-yard algorithm
operator-precedence grammar的特殊情形。常見實現會制定一張 |操作符|^2 的表格。
每個操作符有 in-stack 和 incoming 兩種狀態，判斷優先級根據 in-stack priority 和 incoming priority 即可，可以把 |操作符|^2 的表格簡化爲 2*|操作符|
優先級相等時代表兩端爲 terminal symbol 的 production 的 reduction，比如 `(` 與 `)` 的抵消
Tarjan’s offline lowest common ancestors algorithm
可以在計算LCA的同時處理樹上路徑的monoid查詢
int find(int x)
== x) return x;
;
= find(y);
= mconcat(info 
, info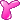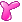 
); // sum of info 
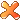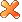& info 
;
{
if (djs
int y = djs
djs
info
return djs
}
void tarjan(int u)
= u; // MakeSet
= …… // sum of path from u to djs 
== -1
== -1
= u
= calculated info of edge (u,v)
`
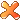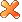, info 
)
{
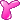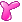djs
info
for each query `q` with one endpoint at `u`
v = other endpoint of `q`
if djs
lca = find(v)
qq[lca] << (query_id, u, v, lca)
for each edge `e` with one endpoint at `u`
v = other endpoint of `q`
if djs
tarjan(v)
djs
info
for each LCA result (query_id, x, y, u) of `qq
find(x)
find(y)
result of query_id = mconcat(info
}
有两本书对《初等算法》影响最大。一本是Chris Okasaki的《Purely functional data structure》另外一本是《算法导论》。写作过程中还参考了一些其他书籍，包括Knuth的《计算机程序设计艺术》，Richard Bird的《Pearls of functional algorithm design》，Bentley的《编程珠玑》以及一些论文。
不足：
写这本书的六年中，我总是想起法国数学天才伽罗瓦最后写的那句话：“我没有时间了！”，我原计划用10年写完这本书，结果提前了4年。这样的代价 很大。为了避免翻译，过滤“噪声”，我直接用英文写作。由于不是native speaker，书中的英文语法和拼写难免贻笑大方。为了赶时间，proof reading被压缩，许多结论采取了“拿来主义”，没有进行严格的数学证明。一些章节的课后习题也没有给出答案。
未来：
理想情况下，一本严肃的算法书应该在稳定、宽松的环境下精雕细琢。可是在社会剧烈发展的今天，在日新月异的中国，在人们习惯快餐而不再享受大餐的 快节奏生活中，在微博、微信取代文章、书信的手机网络大潮下，这样的理想环境根本不存在。未来不可预知。对于《初等算法》这本书，开放给社区是最好的选择。需要做的工作很多：
* 翻译中文版
* 社区proof reading和review，修正内容上的错误和英文上的不足
* 提供一本习题集
* 补足数学证明
* 采用强大的数学工具，对形式化的算法进行分析
一些数据：
《初等算法》黄金分割0.618版本，历时6年，在github上总共提交1680次commit。全书600多页，19万字（word）。2万2千行示例代码。
保护：
《初等算法》在GNU FDL许可协议下发布，所有代码在GNU GPLv3协议下发布。
看《算法导论》，重复看。在略过复杂度摊还分析的情况下，初中数学基础足够弄明白绝大部分内容了。
同样推荐的还有《数据结构与算法分析》，以及邓俊辉老师的MOOC课程《数据结构》。
算法导论这本书，从初三到高二，自己断断续续的看了三年时间。对于算法导论，自己的阅读路径比较曲折艰难，这是当时自己只有中学基础的缘故。好在算法导论 偏向于培养构造性的思维，解题、证明技巧是“算法的方式”而非“数学的方式”，因而得以勉强读了下来。不过平摊分析这样的部分就无能为力了，选择跳过。
循环不变式是算导最开端的内容，也是算法正确性证明最重要的钥匙。本质上，循环不变式是算法归纳证明的形式化。理解算导中每个算法循环不变式的证明过程，就是在理解算法的运行原理。
算导阅读不需要很深的知识储备（你看我这样的初中生也能勉强看）。在看高斯消元LUP分解的时候，我只是通过附录补习了一下矩阵的基本知识，然后就可以看前面的LUP分解算法了。理解算法的正确性是相对容易的，理解算法设计的精妙，反推算法设计的过程难之又难。
代码实现是最好的学习过程。因为竞赛的缘故我使用的是c，当然你也可以用python、java或者brainf**k（雾）。啃完二十多页的二项堆，并且 敲出代码成功运行后，当时的我崩溃的发现还有三十多页的Fibonacci堆在后面等着我。为了记住Fibonacci堆的设计细节，我重复写了20多遍 以至于闭着眼睛都能写出来，结果发现在竞赛中根本用不到，我们有好用又好写的Pairing heap。尽管如此，Fibonacci堆的证明简单而直观，算法设计有趣得很。
尝试修改优化算法导论上的代码。在编写线性规划单纯性 的代码时，我发觉(n+m)*(n+m)的矩阵异常浪费，稍作思考发现可以改成n*m的矩阵加上几个附加向量信息；进一步，对全幺模的情况，可以使用稀疏 矩阵常见的优化方法——链表替代行向量。几个优化过后，我终于可以在竞赛允许的时间、空间、编码量内写一个非多项式的线性规划单纯形算法了。
快 速傅里叶变换也是个有趣的例子。我们都知道，快速傅里叶变换的计算是在复数域上的，而计算机中复数的数值精度会导致FFT在向量比较长的时候丢失信息。后 来学过数论部分，发现复数域是可以由一些特定的模整数运算取代的，于是FFT就可以被用来加速高精度乘法。再后来，发觉这个方法叫做快速数论变换。
每一章的课后习题是检验本章内容是否掌握的准则。如果课后习题有二分之一以上无法独立解决，不妨重新阅读本章内容，给深入思考留些时间。结合习题阅读章节也是可行的。（我记得网上可以搜到部分章节的答案）
说到底，算法导论只是本基础教材，其中无论数据结构、图论，还是动态规划，贪心算法，都只是基础内容。如果看不懂，你需要重新看一下这一章；如果一直看不懂，你需要重新从头读这本书；如果你发觉能看懂了，说明通过培养，你习得了构造性的、“算法”的思考能力。
比如讲到快速排序，很多书可能讲了快速排序的原理就完了。但这本书就直接讲了原始的快速排序可以改进的地方：1. 在小数组上，切换到插入排序；2. 三取样切分；3. 三向切分的快速排序。
优先队列怎么和排序算法扯上关系呢？其实优先队列就是可以用堆排序来实现，堆排序的时间复杂度和快速排序是一样的，但是实际中为什么堆排序的运行时间要比快速排序多呢？因为这和CPU的Cache命中率有关系，堆排序不符合算法运行的局部性原则
还比如书中2.5节，讲了排序算法的实际用途。
这本书不光告诉你算法的原理，还告诉你算法的用途。
这是我在今年求职过程中面试的时候被问到的，因为之前很少接触Streaming的算法，在听到这个题目的时候被惊呆了，根本不能理解：
给一个Streaming的Data，未知长度，要求在Streaming结束后返回N个Data，且是等概率的。
在听到这个问题的时候简直惊呆了。如果Streaming长度已知为L，当然对于每一个Data，我生成一个N/L的概率即可。但是长度未知，也即概率未知，怎么可能在Data来的时候判断要不要保留这个Data，还能保证是等概率的……百思不得其解。
事后一番研究，才发现了这类算法，算法之简单令人惊叹：
首先保留前N个Data，对于后面来的Data以N/i的概率选择是否保留，i为当前Data序号，保留的话在原来保留的N的Data中随机剔除一个。最后返回这N的即可。
证明也很容易，奇妙得地方在于在计算概率的时候，出现了很长的，可以前后上下不断约掉的分式。相互约去之后剩下的概率刚好是N/L，L为总长度。简直美妙极了！
显然这类算法也非常有用，因为在实际问题中会出现大量需要在Streaming的数据中进行Sample，为下一步处理数据做准备的情形。而这竟然有一个O(L)的算法，真是太惊艳了！
首先是KMP和与之相关的AC自动机（Aho-Corasick automaton，刚接触以为是自动AC机），其思想和效率真的很惊艳。
然后是快速傅里叶变换（FFT），可以以的复杂度计算n次多项式乘法。
其次是扩展欧几里得算法，数论题最常用算法了，求乘法逆元、解一次不定方程超级好用，而且代码很短很好记。
再次是快速幂取模算法，理解之后代码很好写，而且效率很高。k阶矩阵的n次方复杂度仅为（不用strassen法加速的情况）。
最后再推荐一个好用但不完全严谨的算法：Miller-Rabin素数测试算法。非常快而且错误率很低啊！
自适应辛普森公式，对三点辛普森公式递归调用的积分算法，代码不到20行，解决所有一维定积分问题。
旋转卡壳算法可以在O（N）时间内求多边形直径。
快速排序算法也是非常好用的，#include<stdlib.h>然后调库是比赛中所有要排序的地方的处理方法，快速排序算法让我惊艳的地方是我去省图书馆看见两个志愿者需要把还回来的一堆书按顺序入架，管理员大妈给他们教的时候说：“你先在这堆书里拉出一本来，把比它号小的扔到一边，比它大的扔到另一边，然后剩下两堆继续这样整，这样排的快！”这是我见识过最惊艳的算法使用，没有之一！
The power of power of 2
下午跟同事吃饭的时候正好聊到一个问题：假设你站在一个足够长的走廊上，在这个走廊的某个位置有一个物品你需要去找到它，请问你应该选择什么样的搜索策略。这个问题的关键在于你不知道目标是在你的左边还是右边，为了保证在线性复杂度内找到它，你可以先向左走1步，回到起点，再向右走1步，再回到起点并向左走2步，……，就这样按照 1，2，4，8，…的等比数列进行搜索，一直到发现目标为止。（虽然在这里2的等比并非是最优的，但这个不重要。）
很简单的思想对吧，但不知当面试时遇到“请问怎么检测一个链表是否有环”的问题时你是否能举一反三呢？我反正是没想到，但是有人想到了，这就是Brent’s Algorithm http://en.wikipedia.org/wiki/Cycle_detection 。这个算法与所谓的标准解法（快慢指针，或者叫做Floyd’s Algorithm）一样优秀（如果不是更好的话，）请务必随身装备，这样下次若有面试官还问你就可以好好秀一把：这个问题我有三种解法blablabla…然后把Brent’s Algorithm丢出去糊他一脸。
2. Fractional Cascading
http://en.wikipedia.org/wiki/Fractional_cascading，史上最酷炫的算法设计技巧没有之一。首先名字就取得非常骚包，其次，还十分有疗效。利用它可以一次性解决计算几何中的一大票问题，比如Orthogonal Range Query，Multiple List Query，Point Location，等等。
3. Rabin Flips a Coin
https://rjlipton.wordpress.com/2009/03/01/rabin-flips-a-coin/。求平面上最近点对的O(nlogn)算法大家都知道，因为算法导论上有写。但是O(n)的算法就没那么多人了解了。Rabin's Algorithm是随机算法中的一个典型代表，看上去直接粗暴，甚至比算导上那个分治法还要简单得多，为什么某名其妙就O(n)了呢？
4. Indirection
5. Amortizing – Deamortizing
我第一次学算法直接看《算法导论》，结果信心大受打击。后来发现Robert Sedgewick在Coursera上出了一系列算法视频教程，把一个算法以动画的形式展现出来，非常适合新手。课程名字就叫Algorithm，普林斯顿大学的，分为Part 1和Part 2。
看视频一边看一边做笔记，看完一个单元跟着把代码写一遍。看完整个教程之后把所有算法都默写一遍，忘记的算法复习一遍。就酱。
正好我也在学算法，初学者，我觉得说在学完一门语言的语法，比如C，比如python后。去了解数据结构还有算法，这是一件很重要的事。
我来分享下我目前的学习经验。
首先刚接触算法时，我看的是《啊哈!算法》。
作者：啊哈磊。曾在中科院玩单片机，在微软亚洲研究院开发“爬虫”，在国际会议上发表论文，也做过老师，是全国青少年信息学奥林匹克金牌教练。
啊哈!算法 (豆瓣)
是C语言的书籍，写的很有趣，非常适合入门读，能够培养你学习兴趣的。
之后可以看的是网易公开课的课程，给上链接
数据结构和算法
小甲鱼的，讲的非常棒，但我目前还没有全部学完~~~~
还有一个是麻省理工学院的公开课
麻省理工学院公开课：算法导论计划详情
最后就是在看经典之作《算法导论》
算法导论 (豆瓣)
好难！！！！！好厚！！！！！需要很好的数学基础。我是一边刷习题，一边百度谷歌。看不懂的只能先跳了，希望这个暑假能先浏览完吧。以后再多看几遍。
第一篇文献一定要多看几遍，细化到每一个公式推导和结论（既然说到公式推导，数学固然重要，泛函，工程数学，工程矩阵论等等时不时要去回顾下），在此基础上编程实现。记住，先看文献再看书，或者说书本只是学习算法的辅助工具，不要花大量时间一个字一个字去细读。等你对经典算法的掌握积累到一定程度之后，可以尝试创新延伸，比如小波变换图像去噪中对方差的估计，将全局方差估计改为局部分子带方差估计，其处理效果是否改善？
推荐《算法导论》，但不是一上来就看，我想强调的有如下几点：
（1）学习算法不是件易事，应该有一个系统化的学习过程；
（2）学习算法要有很好的数学基础，否则学到的算法只能是生搬硬套，遇到实际问题还是不会；（3）学习算法最好的两本书仍然是算法导论 (豆瓣)和算法设计 (豆瓣)。
不管是计算机专业，还是其它专业想自学算法，学习的路线大致是这样的：
阶段一：
基础数学课：微积分，线性代数，概率论
没有微积分极限，收敛等概念，怎么去理解算法中时间复杂度，空间复杂度的概念；不懂矩阵算法中的图算法怎么去入手，不懂概率论随机算法应该不好学，时间复杂度估计算不来。学习书籍可参考学校设的相关课程，概率论的话推荐一本书：概率论与数理统计 (豆瓣)。这三门基础课是一定要学好的。
阶段二：
计算机相关数学：离散数学，图论
离散数学里面有算法，计数，归纳等基本概念，图论里更是囊括了树，图和流的所有理论知识，这些是树，图，流等算法的基础。离散数学推荐书籍：离散数学及其应用 (豆瓣)，图论推荐书籍：图论 (豆瓣)。
计算机相关：C语言，数据结构
数学毕竟只是理论，还得有实际的编程工具，推荐学一门入门的编程语言，C语言最佳（也有高校一上来就学C++或者java的，个人不推荐），还有数据结构更是重中之重，这是你能把树，图能用计算机语言表达出来的基础，我敢说，叫你实现一颗简单的二叉树，你都不一定能写出来，那你还谈学什么算法，数据结构推荐书籍：数据结构 (豆瓣)，C语言和数据结构可以在学习上述数学知识之中穿插着一起学。
阶段三：
系统学习算法，啃《算法导论》吧
其实通过阶段一，阶段二的学习，已经基本掌握了算法相关的所有知识了，那还缺什么呢？系统学习算法，而《算法导论》就能很好的给我们一个学习算法的大框架，深入其中吧，你会发现上面讲的内容你是那么熟悉，但是你的收获又是那么多。在整个过程，可结合《算法设计》这本书一起学，《算法导论》看不懂内容的去《算法设计》上看，两本互补。
阶段四：
算法实践，思维扩展。
到这儿已经没有什么方法而言了，就是多练习，弥补不懂的知识，继续练习，练习题可参考网上的一些算法题集，如leetcode或者ACM题或者各大互联网公司笔试面试题。个人推荐两本书籍：编程珠玑 (豆瓣)，编程之美 (豆瓣)，两本书都有一定难度，但是如果前几个阶段都能做好的话，你获得的一定是趣味。
最后，还是要强调一点，也是我反复强调的，厚积才能薄发，不要浮躁，不要想着看一本书就把算法学好，算法是贯穿整个编程生涯的，毕竟这个式子不是说着玩的：程序=算法+数据结构。
希望大家能静下心来，从最基础的数学知识和数据结构学起，不要贪多，学扎实才是王道。希望大家都能把算法学好，能写出高质量的代码，与大家一同进步，共勉。
设计计算机程序算法和求解数学题有很大的相同之处。程序算法最终要用指令表达，解数学题的方法最终要用数学公式来表达。往往解决问题的根本在于如何想到求解的方法，而不是去记忆求解方法的具体步骤。市面上绝大多数的算法书籍（包括《算法导论》《算法：c语言实现》《编程珠玑》等），基本都仅仅给出了算法的具体步骤、复杂度分析、正确性证明。当我看见快速排序、堆排序、动态规划等让我惊叹的算法时，我总是在想作者是怎么想到这个算法的？但我就是百思不得其解。直到最近我看到了两本书（仅仅看了小部分）才慢慢开始领悟一点点算法设计的奥妙。
1、《算法引论—-一种创造性方法》（建议先看第5章，真是爽爆了）
2、《The Science of Programming》
另外，如果想了解怎么想到求解数学题的方法，建议看看《怎样解题》
去模拟（当然模拟只限于基础的算法)。甚至是手动模拟，比如我之前学深搜，学递归，代码很简单，但是因为涉及到栈，而你的大脑短时间内存储的栈深度只有几层（临时变量越多你大脑能模拟的栈深度就越少），实际上你没办法用大脑去想。比如学习图的深搜，一开始我是不理解的，对递归没办法理解。后来我就在纸上模拟出来，建立好邻接表以后，按照代码步骤一步步纸笔来模拟，慢慢就知道了代码的工作过程。你学习快排也是，当然你背代码也能写出来，但是可能不理解，很快就忘了。《算法导论》书上就有比较细致的执行过程，你手动模拟下partition和quicksort的过程，一开始就用很简单的用例，把整个过程都手动执行一遍，慢慢就了解了。很多算法都有一个循环不变式，你代码如果逻辑正确并且能够维持循环不变式，一般写出来就是正确的。
建议找本《算法》或者《算法导论》这些教材，每学习一个算法就先大致浏览下， 然后细致分析每一步代码的执行过程（纸笔模拟或者代码单步调试），当确认你真正明白之后，尝试不看代码就靠对算法过程的了解和正确的逻辑去自己实现。
当然，我不认为你写出很多算法就是高手了，现在大部分高级语言不需要你重复造轮子，你造出来的质量也远逊于库中那些高手的代码，可以去学习他们代码的实现，比如看看stl源码。真正工程用到的代码与一般算法实现还是有很多改进的。
最重要的不是你会写这些算法了，而是学会了很多思想。比如二分的思想，递归的思想，分治的思想，动态规划，贪心等，以及现实中很多数据结构的抽象等。难的不是学会了算法，而是如何运用这些算法思想去解决问题。
我记得大一学校有个什么数学建模班，作为考试入班需要提交一个程序解一大堆应用题中的一个。彼时算法课计算机系还没有教，其他系更不用说。但是还是有各种人物用自发明的各种算法加上自学的C和C++把各种问题都啃下来了。不用任何框架直接C++/COM加3D碰撞检测的DirectX游戏照样有人做出来，还不是计算机系的。我那时觉得已经到我脑力极限的DirectX/OpenGL英文手册在他看来和日漫一样简单必须是数论变换,我不嫌丢人,看到这个算法之前我根本不知道数论能干吗用.
一个基于数论的变换,把整数域变换到整数域,居然能和FFT形式上一致,还和定点DSP
结合得这么好,连乘法器都不用,直接移位就能快速算卷积,惊了! 当时是在图书馆的一个
很破,旧的发黄的书上看到的,当时有一种摔下悬崖无意中发现了武功秘籍的感觉
伪随机算法 （Pseudo Random Distribution，简称PRD，不是需求文档!）
暴击真的看脸吗？当然不是了，当你深刻理解了伪随机算法，我想你还是可以对暴击进行一些人为干预的。这个时候就是你 dota 水平迈向另一个境界的时候了。
伪随机跟真随机有什么区别呢？来举个例子吧，假如剑圣的暴击几率为20%，那么真随机的情况下，系统随机在1~100里面生产一个整数，如果生成的整数小于等于20，那这次攻击就判定为暴击。这个时候就有可能出现连续5次攻击全是跳劈，脸黑得选手可能连续10次攻击也没有一次暴击。而极限的情况就是，你的BM或者PA可能一整场都在暴击（卧槽，你丫开挂呢），或者你打完一整场都没暴击过一次（艹，简直猪队友啊）。而伪随机呢，就是用来解决「减少连续性暴击，减少连续性没暴击」这个问题。
还是拿剑圣20%暴击概率举例，这时候剑圣第一次攻击暴击的概率是5.57%，而下次的攻击就会是11.14%，如果第二次还没暴击，那么接下来的第三次攻击的暴击概率就提升到了16.71%，每次都加5.57%，直到第17次攻击就会是100.26%的保证性暴击（ (⊙o⊙)…，好像还真有脸黑的情况存在）。暴击之后回到之前的5.57%，这样在多次的攻击后会形成个平均20%暴击的几率。
以下使用PRD机制的列表
进攻类，暴击、重击、双刀、漩涡
防御类，山岭的皮肤，所有盾类
不受PRD机制控制的物品有
碎骨锤，深渊之刀的晕，蝴蝶/天堂之戟的闪。
概率公式
P(N) 表示在第N次攻击之后某个动作发生得概率（下面还是以暴击举例吧），N表示第N次修正概率后得攻击次数（最小值为1），C表示暴击发生的初始概率以及每次攻击之后概率的增量，是个简单地线性关系。当N足够多得时候，P（N）总会趋向于1。在以下的文章里，技能描述上的概率会以 P(E) 来代替，表示期望值。
PRD 常数C
以下有两个表来描述常熟C。P(E)表示期望值，C是常数。MAX N表示 理论上叠加到100%暴击之前的最后一次攻击次数，举个例子，如下表，比如的暴击几率是45%，C是0.24931，那么N就是4，因为之前的连续4次攻击都可以是普通攻击，但第五次的时候，必定暴击。
当然以上得理论值不是暴雪实际中应用的数值，实际应用是如下表
在上面表中可以发现，当暴击几率到一定值得时候，实际暴击几率就低于P(actual)就低于P(E),这后面就会涉及到暴击收益递减的问题，这里就不深入讨论了，必定dota里面的暴击好像也不是那么好堆，像 WOW 里面倒是可以讨论一下。
再把两个图放一起对比，好好感受一下。常数C在在30%的时候实际值跟理论值还是很接近的，但是超过这个值以后，误差就开始大了。
那么引起这个概率偏差的原因是什么呢？简单归纳是由以下两点因素造成的
1.常数C的有效位数。我们可以从上面的表格中看到，在实际运算中我们没有采用无线有效位而是取了一个近似的5位小数点，造成了之后的误差。如果是采取动态实时运算的C的话，这会在每一次攻击动作的判定都会耗费非常多的CPU资源，因此选取了一种静态的look up table。
2.所有的数值都是会天梯地图准备的，而不是普通用户自己编辑的地图。我们可以发现天梯地图里面技能概率值最大的特殊攻击是牛头人的粉碎，25%，再回头看看，在30%以下，实际技能触发概率和期望概率是基本一致的，30%以后的C值都是在用之前的数据拟合出来的。而且说实话，暴雪粑粑目前也不在意这些情况。